Fractales para crear naturaleza por ordenador

Los fractales se generan a partir de algoritmos recursivos. Pero, ¿qué es la recursividad?. Es un concepto difícil de entender porque para comprender la recursividad primero hay que entender la recursividad. Bromas aparte, la recursividad es la autorreferencia de algo hacia sí mismo. Un ejemplo muy simple para apreciar la recursividad es colocar un espejo frente a otro. En un algoritmo consiste en hacer que, en algún punto dicho algoritmo, se llame a sí mismo. Esto permite crear comportamientos y estructuras complejas con algoritmos muy simples. Un buen ejemplo de ello es el fractal de Koch, que consiste en crear una estructura geométrica dentro de la cual vamos a repetir esa misma estructura:

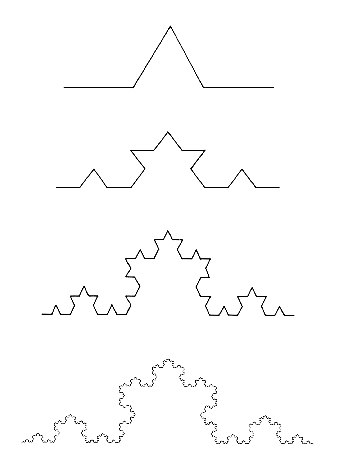
Esta es una manera de proceder que era de esperar en la naturaleza. ¿Cómo si no iban a poder unos pocos genes recrear la riqueza del sistema circulatorio del cuerpo y otras muchas estructuras complejas de los seres vivos, si no es porqué estos genes están codificando un algoritmo recursivo muy simple?

El nombre de fractal lo acuñó Benoît Mandelbrot. Éste desarrolló y popularizó esta disciplina gracias a los primeros trabajos en este campo de Gaston Julia. Mandelbrot pudo generar sus primeros fractales porque, en ese momento, era una de las pocas personas en el mundo que disponía de ordenador, al trabajar para IBM.

La introducción de su libro "La geometría fractal de la naturaleza" de 1982 dice así:

"Las nubes no son esferas, las montañas no son conos, los litorales no son circulares, y los ladridos no son suaves, lo mismo que los relámpagos no van en línea recta".

Podemos encontrar fractales en todas partes, las costas, los afluentes de los rios, los caballitos de mar, las hojas, ramas y raíces de los árboles, los copos de nieve, el brócoli, la coliflor, el romanesco, etc.

A continuación podéis disfrutar de un video reciente del propio Benoît Mandelbrot (podeís activar los subtitulos en español):

Ver en TED

En el video, Mandelbrot habla de la dimensión de Hausdorff o fractal. En la geometría ordinaria tenemos objetos de una, dos o tres dimensiones mientras que, en la geometría fractal, las dimensiones tienen decimales. Por ejemplo, decir que un objeto fractal tiene dimensión de 1.33, indica que tiene una dimensión (es una línea) y los decimales, como bien explica Mandelbrot en el video, representan la rugosidad de ésta. Cuánto más alto sea el decimal más rugosa será la linea.

La forma de dibujar el conjunto fractal de Mandelbrot es relativamente simple. Usa esta fórmula recursiva:

Resultado actual = (Resultado anterior)^2 + constante (donde el resultado anterior inicial es el cero)

En esta pagina, he hecho un pequeño programa para que podais ver el conjunto de Mandelbrot. Funciona de la siguiente manera: Se toma como valor de la constante un número complejo (está compuesto por una parte imaginaria y una parte real). Si el valor elegido para la constante hace que la fórmula tienda a infinito, no pertenece al conjunto, de manera que pintamos ese punto en negro. Sino, matemáticamente se dice que tiene límite o que está acotada. Ese punto se pinta de verde ya que pertenece al conjunto.

Por ejemplo, si la constante es igual a 2+0i, la fórmula tiende a infinito ya que obtenemos cada vez números más grandes (2,6,38,...), por tanto, en el punto x=2 (parte real de 2+0i) e y=0 (parte imaginaria de 2+0i) del plano complejo, pondremos ese pixel en negro. De esta manera, iremos dibujando el resultado, recorriendo las coordenadas "x" e "y" de la pantalla asignándoles valores a la constante compleja para cada posición.

En la práctica, como no se pueden calcular infinitos valores para comprobar que este tipo de serie tiene límite, se considera que la fórmula tiende a infinito si llega a superar un cierto valor durante un determinado número de iteraciones.

Como premio por haber llegado al final de esta entrada, tenéis un viaje 3D por el conjunto de Mandelbrot:

Ver en Youtube

Los fractales también aparecen al representar gráficamente las variables de sistemas dinámicos caóticos, aunque en estos casos es más correcto llamarlos atractores extraños. Representar estos atractores en un ordenador permite estudiar como se comportará el sistema en un futuro cercano, pero de eso ya hablaré en otra entrada.